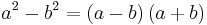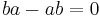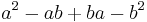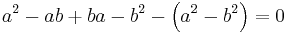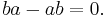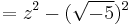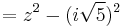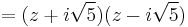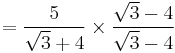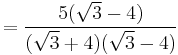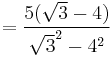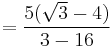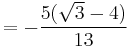Difference of two squares
In mathematics, the difference of two squares, or the difference of perfect squares, is when a number is squared, or multiplied by itself, and is then subtracted from another squared number. It refers to the identity
from elementary algebra.
Contents |
Proof
The proof is straightforward, starting from the RHS: apply the distributive law to get a sum of four terms, and set as an application of the commutative law. The resulting identity is one of the most commonly used in all of mathematics.
The proof just given indicates the scope of the identity in abstract algebra: it will hold in any commutative ring R.
Also, conversely, if this identity holds in a ring R for all pairs of elements a and b of the ring, then R is commutative. To see this, we apply the distributive law to the right-hand side of the original equation and get
and if this is equal to 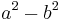 , then we have
, then we have
and by associativity and the rule that  , we can rewrite this as
, we can rewrite this as
If the original identity holds, then, we have 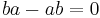 for all pairs a, b of elements of R, so the ring R is commutative.
for all pairs a, b of elements of R, so the ring R is commutative.
In geometry
The difference of two squares can also be illustrated geometrically as the difference of two square areas in a plane. In the diagram, the shaded part represents the difference between the areas of the two squares, i.e. 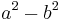 . The area of the shaded part can be found by adding the areas of the two rectangles;
. The area of the shaded part can be found by adding the areas of the two rectangles; 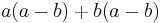 , which can be factorized to
, which can be factorized to 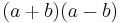 . Therefore
. Therefore 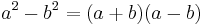
Another geometric proof proceeds as follows: We start with the figure shown in the first diagram below, a large square with a smaller square removed from it. The side of the entire square is a, and the side of the small removed square is b. The area of the shaded region is 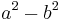 . A cut is made, splitting the region into two rectangular pieces, as shown in the second diagram. The larger piece, at the top, has width a and height a-b. The smaller piece, at the bottom, has width a-b and height b. Now the smaller piece can be detached, rotated, and placed to the right of the larger piece. In this new arrangement, shown in the last diagram below, the two pieces together form a rectangle, whose width is
. A cut is made, splitting the region into two rectangular pieces, as shown in the second diagram. The larger piece, at the top, has width a and height a-b. The smaller piece, at the bottom, has width a-b and height b. Now the smaller piece can be detached, rotated, and placed to the right of the larger piece. In this new arrangement, shown in the last diagram below, the two pieces together form a rectangle, whose width is 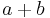 and whose height is
and whose height is 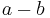 . This rectangle's area is
. This rectangle's area is 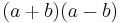 . Since this rectangle came from rearranging the original figure, it must have the same area as the original figure. Therefore,
. Since this rectangle came from rearranging the original figure, it must have the same area as the original figure. Therefore, 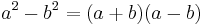 .Any odd number can be expressed as difference of two squares.
.Any odd number can be expressed as difference of two squares.
Uses
Complex number case: sum of two squares
The difference of two squares is used to find the linear factors of the sum of two squares, using complex number coefficients.
For example, the root of 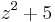 can be found using difference of two squares:
can be found using difference of two squares:
Therefore the linear factors are 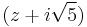 and
and 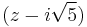 .
.
Since the two factors found by this method are Complex conjugates, we can use this in reverse as a method of multiplying a complex number to get a real number. This is used to get real denominators in complex fractions.[1]
Rationalising denominators
The difference of two squares can also be used in the rationalising of irrational denominators.[2] This is a method for removing surds from expressions (or at least moving them), applying to division by some combinations involving square roots.
For example: The denominator of 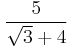 can be rationalised as follows:
can be rationalised as follows:
Here, the irrational denominator 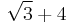 has been rationalised to
has been rationalised to 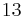 . Any odd number can be expressed as difference of two squares.
. Any odd number can be expressed as difference of two squares.
See also
References
- ^ Complex or imaginary numbers TheMathPage.com, retrieved 22 December 2011
- ^ Multiplying Radicals TheMathPage.com, retrieved 22 December 2011